Data Display and Summary
Lecture 1

The t Distribution

1. Types of data

   1. Quantitative variables – how much

      1. Continuous variables – business profits, sales, etc

         • Various in range

      2. Discrete – counting things

         • Number of factories, workers, etc

   2. Categorical variables – what type

      1. Unordered – also called nominal

         • Gender – male and female

      2. Ordered – also called ordinal

         1. Grades – A, B, C, D, and F

         2. Class level – 1 ^st, 2 ^nd, 3 ^rd, and 4 ^th

         3. Responses on a survey

   

   1. Possible to convert one variable into another

      • Example: Weight for a male

        • > 150 Kg “Very fat”

        • 75 < and < 150 Kg “Fat”

        • Etc.

2. Stem and Leaf Plots

   1. Data should be plotted to get an idea what it looks like

   2. This method is old

   3. Example: Company’s assets in $ billions

      1. Data – 3.5, 6.9, 4.4, 4.4, 2.2, 5.3, 4.3, 4.0, 5.1, 7.1, 0.6, 5.3, 6.7

      2. Scan data and find the smallest and largest numbers

      3. The data is unordered

4. The data is ordered

1. Outlier – an extreme value

2. Benefit? – The only plot where we still have the original data

3. Median – a mid point of a data set

   1. Take data and order it from smallest to largest

   2. Example

      1. Unordered: 4.5 6.3 6.1 5.5 7

      2. Ordered: 4.5 5.5 6.1 6.3 7

   3. The median is the value in the center, which is 6.1 in our case

   4. The median is not sensitive to outliers

   5. If the data has an even number of points, then take the average of the two points in the center

   6. Example

      1. Unordered: 3 10 8 7

      2. Ordered: 3 7 8 10

      3. The median is the average of 7 and 8, which is 7.5

      4. The average is (7 + 8)/2 = 7.5

4. Measures of variance

   1. Range – the difference between the largest value in the sample (the maximum) and the smallest value (the minimum),

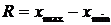
1. 1. Very sensitive to outliers

   2. Example

      1. Unordered: 5 4 6 7 100

      2. Ordered: 4 5 6 7 100

   3. The range is [4, 100]

   4. Did you notice the 100? It appears to be an outlier, because it is very large relative to the other numbers

2. Quartiles – divide the data into four groups

1. 1. Usually works well for large data sets

   2. Box-Whisker Plots – a nice way to plot quartiles

      1. Excel cannot do this!

      2. We can have several Box-Whisker Plots side by side

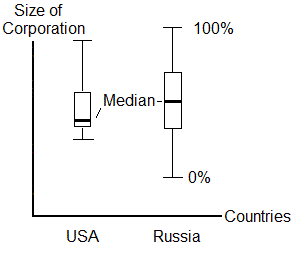
1. 3. Some statistical programs can calculate these

5. Histograms – for continuous variables

   1. Excel can do this with some difficulty

   2. Steps

      1. Take the data and categorize into groups; groups are ranked

      2. Count how many are in a group, which is the frequency

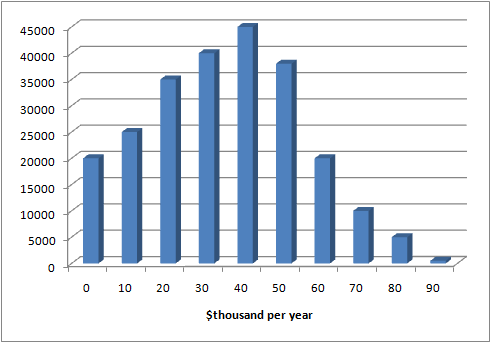
3. A histogram displays the distribution of data

4. Excel

   1. Find the maximum data point by using =max( ) function

   2. Find the minimum data point by using = min( ) function

   3. Specify the number of categories, k, which are also called bins

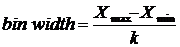
     First category: min. to min. + (width)(1)

     Second category: min. + (width)(1) to min. + (width)(2)

     Last category: min. + (width)(k – 1) to min. + (width)(k)

4. Then use =countif( ) function to count how many data points fall with a category

   1. This part is hard

   2. Excel has a histrogram function in Data Analysis

5. If you choose too many categories, then you get noise

6. Bar charts – categorical data

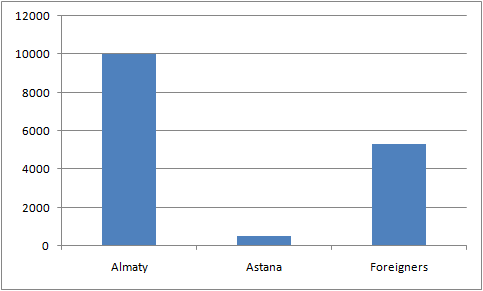
   1. Example – Medeo collects information on visitors for 2008

      1. Almaty has 10,031 visitors

      2. Astana has 542

      3. Foreigners who visited are 5,321

2. Could convert frequency into a percentage